Anton V. Leouski and Paul E. Utgoff
Technical Report 96-10
January 20, 1996
Department of Computer Science
University of Massachusetts
Amherst, MA 01003
Telephone: (413) 545-4843
Keywords: Neural network, game-playing, temporal difference learning
Conventional Othello programs are based on a thorough analysis of the game, and typically employ sophisticated evaluation functions and supervised learning techniques that use large expert-labeled game databases. This paper presents an alternative method that trains a neural network to evaluate Othello positions via temporal difference (TD) learning. The approach is based on a network architecture that reflects the spatial and temporal organization of the problem domain. The network begins with random weights, and through self-play achieves an intermediate level of play. We also present a simple and effective method for analyzing what the network learned.
The game of Othello is a descendant of an old Japanese board game. Like chess, it is a deterministic, perfect information, zero-sum game of strategy between two players. The limited length of the game, typically sixty moves, and the small average branching factor, approximately seven, give Othello a complexity greater than checkers but less than chess. This complexity, which causes any attempt to find an exact solution on today's computers to fail miserably, and the alluring simplicity of the rules make the game an attractive domain for experimenting with automatic learning methods.
Various learning methods such as Bayesian learning [Lee and Mahajan, 1988, Lee and Mahajan, 1990] and genetic algorithms [Moriarty and Miikkulainen, 1993] have been applied previously to this domain with varying degrees of success. In this paper we present a different automatic technique for learning Othello strategy. Of interest are the extra steps in network engineering that were needed to improve the program's learning.
This method is based on training a neural network via Temporal Difference (TD) learning [Sutton, 1988]. Tesauro demonstrated success with this approach with his TD-Gammon [Tesauro, 1992, Tesauro, 1994], which plays backgammon at a World-Championship level. That work has prompted many several researchers, including us, to apply this technique to other game domains [Walker, 1992, Brockington, 1995]. The first report [Walker, 1992] of a straightforward application to Othello was discouraging. The neural network, whose input was a raw board configuration, was unable to advance beyond a novice level. Existing good Othello programs use a number of human-engineered high-level features, so one may surmise that the neural network was not able to find these.
In this paper we present three different neural network architectures for Othello, and compare them empirically. The simplest network achieves only a novice level of play, and the most complex network achieves an intermediate level. We show that incorporating spatial and temporal characteristics of the domain into the network structure results in creating a more accurate evaluation function. The overall training process becomes more effective and stable.
In addition to describing and comparing the three networks, we present a simple method for analyzing what the network learns. This analysis technique indicates that the most advanced network learned not only the weighted-squares strategy, but also certain patterns related to the concept of immediate mobility.
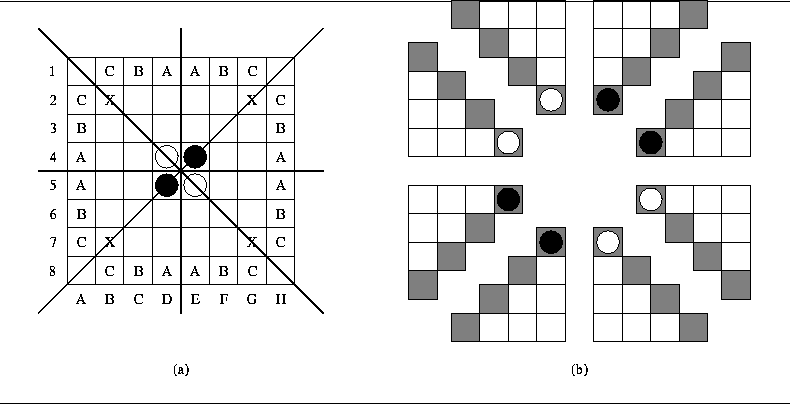
Figure 1:
(a) shows the eight traingles of an Othello board; it also shows
the initial board setup and standard Othello square notation;
(b) shows the same eight triangles separately. The diagonal squares are
shaded to emphasize that these squares are shared by two triangles.
Othello [Brockington, 1995] is played on an 8-by-8 grid, using dual-colored black-and- white disks. Black commences play from the initial board configuration shown in Figure 1(a). A legal move for a player is the placement of a piece on the board resulting in the capture of one or more opponent's pieces. A capture occurs when a player places a piece of his color in a blank (empty) square adjacent to a line of one or more pieces of the opposing color followed by a piece of his own color. Captured disks are not removed from the board, but are instead flipped to the captor's color. Play continues until neither player has a legal move, which usually happens when the board is completely filled. At the end of the game, the pieces of each color are counted, and the player with the greater number of pieces is declared the winner.
Our investigation led us to try three different network architectures for Othello.
We begin by considering a classical fully-interconnected neural network with one hidden layer, similar to the network created by Walker [Walker, 1992]. The network has 64 input units corresponding to the 64 squares of the Othello board. Each input unit outputs a value of +1, 0, or -1 according to whether the corresponding board square contains a black disc, no disc, or a white disk.
The network is fully-interconnected at each level. This means that the output of every input unit is an input to every hidden unit, and the output of every hidden unit is an input to the single output unit. In addition, every hidden unit has a connection from a bias unit that always assumes value +1. The output of each hidden unit is the linear combination of its inputs squashed by a sigmoid function. If x is the linear combination, then
is the output of the hidden unit. This is a standard method for constructing a non-linear activation function. The hidden layer has 55 units, which was determined by trial-and-error. The single output unit also has a bias connection and sigma activation function.
Figure 2:
(a) ten input units of a board triangle form a hidden unit;
(b) eight triangles form a feature map.
The second network takes into account the symmetry of the board, which is a spatial property of the domain. Every position is invariant under rotation and reflection. The relative positions of the pieces and board edges are always preserved. This causes certain sets of squares to form equivalence classes. For example, the four corner squares form a class. So too do the eight squares that are vertically or horizontally adjacent to a corner square (called the `C' squares). There are a total of ten such equivalence classes, indicating that there are ten distinct kinds of squares on the board.
Consider an Othello board, as shown in Figure 1(a). If we break the board into 8 pieces by straight lines, it will result in eight triangularly-shaped groups, as shown in Figure 1(b). Every triangle consists of the ten kinds of square. The triangle is an invariant for reflection or rotation of the board. The pieces inside one of the triangles would not be affected by either rotation or reflection. The relative positions of the triangles with respect to each other are also preserved. We want the network to reflect this symmetry. It should react the same way (output the same number) on two different boards produced by rotation and/or reflection. To achieve this we incorporate the technique of weight-sharing described by Rumelhart et al. [Rumelhart, et al., 1986], and used successfully by Le Cun et al. [Le Cun, et al., 1989].
Every board square has a corresponding input unit in the neural network. Recall that the output value of each unit is 1, 0, or -1, depending on whether the square is occupied by black, is empty, or is occupied by white. You may imagine that the input units are also arranged in the 8-by-8 grid and that this grid could also be broken into eight triangles with ten units each. We connect all input units from one triangle to one unit in the hidden layer, as shown in Figure 2(a). Eight hidden units connected to the different triangles form a plane that Le Cun et al. [Le Cun, et al., 1989] call a feature map, as indicated in Figure 2(b).
We want the total output of a feature map to remain the same if we rotate the board. Therefore, every unit in the feature map must represent the same function of its input units. This is achieved by input weight sharing among units in the feature map. For example, there are eight input units corresponding to the different B-squares on the board. Each one is connected to a different hidden unit in a feature map. Weight sharing guarantees that all these connections have the same weight value.
Several feature maps define the hidden layer of the network. All units in the hidden layer are connected to one output unit. All hidden units and the single output unit have a bias connection and a sigma activation function. In our experiments the network has twelve feature maps. Thus, we have 64 input units, 96 hidden units, and one output unit.
An analysis of the game of Othello [Rosenbloom, 1982] shows that it has at least three rather distinguishable stages: opening-, middle-, and end-game. Every game stage lasts approximately twenty moves and it is believed to have a unique strategy. For example, mobility (number of legal moves) plays an important role during the middle-game, whereas the number of discs owned becomes the main factor toward the end. Training one network to evaluate board states in different game phases is the same as training the network to perform different tasks at different times. The network can become a victim of the effect of temporal crosstalk [Jacobs, 1990]. Thus, it seems reasonable to have a different network trained for every game phase.
The disk count provides a good approximation of the game state [Lee and Mahajan, 1990]. We designed the third network as a supercomposition of three different networks from the previous section. In this composition the coefficients, which are also called application coefficients [Berliner, 1979], are functions of the disc count. To smooth the transition between the game phases we choose a sufficiently smooth function:
where 
=20, and 
assumes values 4, 34, and 64.
Therefore, Network 3 has 64 inputs, 96x3=288 hidden units, and three output units. Despite its complex architecture it has approximately the same number of connections as Network 1. Thus, all computations take the same time for both networks.
Figure 3: Learning curves for three networks over 15,000 training games
Every network was trained by playing against itself for over 15,000 games. The weights were initialized to uniform random numbers in the range [-1,+1]. The following formula was used to update the network weights:
where 
is the learning rate. A value close to 0.1 is generally
used, since higher learning rates degrade performance, whereas lower
rates reduce fluctuations in performance [Sutton, 1988, Tesauro, 1992]. We set
to 0.05. We also chose to set 
to 0, implementing TD(0). was
The 
is the current prediction, the output of the
network given the current board state. The next prediction, the
is the result of the minimax search performed to the depth
of two. At the end of the game, when there are fewer than eleven empty
squares left, an exhaustive minimax search is performed and the
is the difference in disc counts for both opponents divided
by ten and squashed with the same nonlinear function used in the
network:
The weight changes are accumulated as the game progresses and the actual update is performed after the game is over.
The sigma function scales the final reward to the same range of values as the intermediate prediction values. Also, the particular shape of the function enforces the condition that the more discs the program wins/loses at the end of the game, the less important it is to predict the exact disc count.
Figure 4: Smoothed learning curves for same three networks over same 15,000 training games
Unlike backgammon, Othello is a deterministic game, so to ensure
sufficient exploration of the state space, a stochastic factor was
added to the learning process. Consider a game state encountered
during the search. Suppose, it has n children and 
is the
evaluation for the ith child. Suppose also that we have evaluated
m;SPMlt;n children so far, with best being the child with the highest
value encountered so far ( 
), and suppose
that the next child is better ( 
). Then, we keep this
next child as the new best ( 
) with probability
0.9.
The performance of the networks was measured by running them against
another Othello playing program named Wystan
, which uses an evaluation function
that incorporates several high-level features such as mobility and
stability. The games were started from several different positions
generated as follows: start with the initial board setup. All
combinations of the four first legal moves from this position will
result in 244 different board states. Discarding the boards that are
equivalent with respect to rotation and reflection we are left with sixty
unique positions. Both programs played sixty games starting from these
positions. The number of games won by the network was recorded as the
performance measure.
Every network was trained for approximately 15,000 games. At intervals of 120 training games the learning was switched off and the network competed against Wystan. Figure 3 shows the learning curves for all three networks. Figure 4 shows the same learning curves smoothed. Network 1 loses to Wystan more than 60% of the time. Network 2 shows approximately the same degree of performance as Wystan. Network 3 defeats Wystan more than 75% of the time, with a best recorded result of 54 out of 60 victories. Network 3 shows markedly improved performance over Network 1.
Analysis of Network 3's play reveals that it appears to know to avoid an X-square when necessary and yet take an X-square when it is advantageous. It also behaves as though it has the concepts of mobility and stability along the edges. However, we were not able to discern such a concept by inspecting the weights. An alternative explanation is that by owning certain discs, say near the center, and not owning other discs, say further away from the center, the side effect is to attain better mobility than the opponent.
We have also done an informal comparison of Network 3 against LOGISTELLO
- the current World Champion among
computer Othello players. The program that used 2-ply search achieved
an easy victory against 1-ply LOGISTELLO though it was defeated by 2-ply
version of the Champion.
A neural network with one output unit represents a non-linear
multivariable function 
, where the arguments
are the outputs of the input units. In our
case 
is the value for i-th square on an Othello board. It
assumes values +1, 0, or -1, depending upon whether the square is
occupied by a network's disc, is empty, or is occupied by an opponent's disc.
The immediate analysis of such a function is usually difficult due to
the complex nature of the neural network. We approximate 
with a polynomial, for example, by using a Taylor decomposition:
where an n-th order coefficient is defined as
The advantage of this approach is that 
could be
easily interpreted in a conditional form ``if the 
square is
occupied by ... and 
square is occupied by, and ..., then add
this amount to the final board evaluation.'' For example, 
defines the independent contribution of to .
These coefficients define the relative importance of the interactions
among squares. The values should be interpreted as `better' or `worse',
not `good' or `bad'.
The remainder ( 
) is important. For every coefficient there always will be a
coefficient of a higher order 
that will modify
the original one if and only if 
.
However, for our purposes it is sufficient that this modification be
much smaller than the coefficient itself. Our estimations show that
decreases as n increases.
Figure 5: Depiction of first-order coefficients for Network 3
The first-order coefficients can be visualized as an 8-by-8 grid of black and white squares, as shown in Figure 5, where every square corresponds to a location on an Othello board. The area of the square is proportional to the absolute value of the coefficient. The white and black squares represent positive and negative values respectively.
Figure 6: Depiction of first-order coefficients for four most important feature maps in the first network of Network 3
Figure 5 shows the first-order coefficients computed for the three networks that form Network 3. The leftmost picture defines the network that is most responsible for an opening game stage, the second one - for a middle-game, and the third one - for an end-game. Each one of these pictures roughly represents the weighted square strategy [Rosenbloom, 1982], with a high positive value assigned to the corner squares and high negative value assigned to the X-squares. One should notice that taking an X-square becomes less unfavorable as the game progresses, which is due to the fact that the more discs that are on the board the less chance there is that taking an X-square will lead to the loss of a corner.
Figure 7: Depiction of first-order coefficients for four most important feature maps in the second network of Network 3
To see what features the feature maps have discovered we performed the same analysis on each feature map separately. Figures 6 and 7 show the most valuable four feature maps (the feature maps with the highest absolute values) from the first and the second networks. Some of these features are rather easy to interpret. For example, the second and the third maps in Figure 6 suggest one stay inside the central 16 squares during an opening. The third and fourth maps in Figure 7 suggest one capture the edges, however avoiding C-squares.
Figure 8: Depiction of second-order coefficients for squares A8, B8, C8, and D8 in the third network of Network 3
Next we describe some observations made for the second-order coefficients. Figure 8 shows the interactions of squares A8, B8, C8, and D8 with the rest of the board computed for the third network. For example, consider the interaction between A8 and B8:
where 
could be found in the first picture as the second
square from the left in the bottom row. It is relatively big and
black. We can interpret this result as ``it is relatively
unprofitable to have two discs of the same color on both A8 and B8.''
If this rule sounds counterintuitive, consider the interpretation ``it
is much worse to have two of your opponent's discs on both A8 and B8,
than to have the opponent's disc on A8 and your disc on B8.''
Each picture on Figure 8 is drawn in its own scale and has corner coefficients removes due to their high values. Notice that the corner square affects, for example, all X-squares almost the same way, and C- and A-squares affect mostly only the closest X-square. We say that a corner is important for the whole board position and C- and A-squares are just locally important.
Figure 9:
Left: black has a move at C1; Right: square C1 already taken.
There is some evidence that the network may have acquired some notion of immediate mobility. For example, suppose the network plays black. The lefthand position of Figure 9, where black has a move at C1, will generate a significantly larger value than the righthand position of Figure 9, where C1 is already taken.
Figure 10: Two different boards that generate the same response from Network 3.
Our results show that incorporating spatial and temporal properties of the domain into the network architecture improves its performance. However, this is achieved with some loss of sensitivity in the network. For instance, Figure 10 shows two very different boards that would generate the same response from the network. This problem could probably be solved by considering pattern types other than the triangles we used [Buro, 1994].
The second observation we make is that the game is not as symmetric as we have assumed. The fixed initial setup (Figure 1(a)) suggests that Othello positions are symmetric only to rotation by 180 degrees and/or reflection relative to a diagonal.
The third observation is that we defined a game stage by the total number of pieces on the board. This assumption is valid while the game is progressing evenly from the center to the edges. However, as this progression breaks down and the game begins to concentrate on one side of the board, this heuristic fails. For example, consider a game where all moves were made on the left side of the board. After roughly 30 moves the left side will be almost filled with discs, when the right side will be almost empty. The game on the left side is almost over, when on the right side it is just beginning. The network must be totally confused by such setup. A possible solution is to consider gating networks [Jacobs, et al., 1991] as the mechanism for setting the values of the weights on the connections between the input and hidden layers.
We conclude that:
